|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||
| The “Fall” of Bodies | The “Fall” of Bodies
Fabio Bevilacqua - Stefano Bordoni ABSTRACT: We present a “case study” for school students. Our aim is not to train students to the Galilean-Newtonian truth but to offer them a journey through history of physics. With the help of multimedia and hypermedia tools, they can meet the phenomenon “The fall of bodies” together with the different explanations offered by great scientists: Aristotle, Galileo, Newton and Einstein. During the journey, students become aware both of phenomenology and of alternative interpretations of this phenomenology. Physics does not deliver a final truth, but allows us to join a more exciting adventure: the endless effort toward a better understanding of nature. |
||||
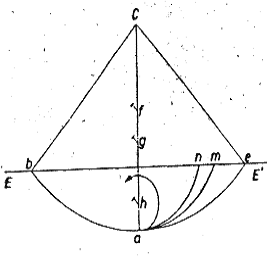
| Galileo’s inclined plane experiments | |||||
Imagine a person lifting two different objects with his/her hands and keeping them at the level of his/her shoulders, with open arms. In general, for different materials, even though the two bodies have the same shape, he/she would experiment on his/her arms two different efforts. Imagine then that person is tired: he/she open his/her hands at the same time. What happens? Educational researches show the problems students have in acquiring the “Galilean-Newtonian” point of view on “free fall” and the persistence of “alternative” conceptions still echoing the Aristotelian paradigm.
Actually, Einstein’s theories are almost a century old but are still waiting for the pedagogical role they deserve. From this point of view, usual textbooks appear as useless repository of dogmatic statements whose origin is not explained and whose meaning is hidden under the attempt at establishing a quantitative correspondence among them. In the spirit of this series of conferences, an attempt will be made here to utilize history of physics to improve matters. This will benefit, I believe, from the use of modern technologies, namely hypermedia (hypertextual interactivity joined with the use of different media). Quantitative simulations are in the case of “free fall” especially useful: far from being a substitute for real scientific experiments they offer a simple, far reaching and economical tool to visualize different world views and perform thought experiments. In this approach, the first step is the perception of the “phenomenology” of “free fall” as independent as possible from theoretical interpretations. In standard conditions, between two bodies that are left “free” from the same height at the same time, the heaviest body reaches the ground first, even if the shape of the two bodies is the same. This is at variance with the motions of cosmic bodies: they do not seem to fall and their drifts - except for the sun - are very slow. The speed of fall, in general, prevents us from doing a detailed experimental analysis, but through a simulation this phenomenology is easily reproduced. Due to the dilatation of the computerized time scale, the events are easily observed. At this stage we will offer a story to lead students travel through history of physics, making them meet the great scientists and their theories. The main characters of the story will be Aristotle, Galileo, Newton and Einstein. They produced the scientific theories which more influenced western culture. We have two basic aims:
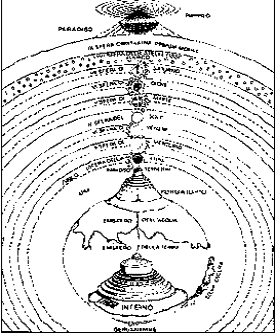
1) Aristotle |
|||||
Fig. 1 |
Fig. 2 |
||||
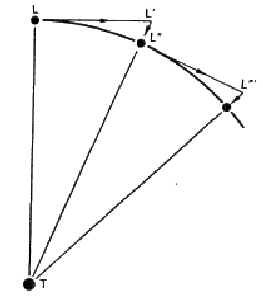
Indeed, the “natural” motions are just the motions toward the natural places. “Violent” motions are the ones which eject bodies from their natural places. Natural motions do not require any cause; the causes required by violent motions are always directly applied to bodies. The depletion of these causes make bodies return to their original place. Different kinds of motion cannot exist at the same time in the same body. We could consider the motion of an arrow from the point of view of Aristotle: it moves because the strength of the bow is transmitted to the air, which continue to push the arrow, until the complete depletion of the strength. At this point, the arrow begins to fall, to reach its natural place. The two motions are subsequent: concepts like “sum of velocities” do not exist in Aristotle’s physics. This is coherent with his general idea: a mathematical operation could not be applied to physical events. The complete path of the arrow is closer to a right angle than to a parabola. (See in fig. 3 the example of an air balloon) |
|||||
Fig. 3 |
Fig.4 |
||||
Aristotle stated that different bodies fall with different velocities: velocity depends on their weights. Greater is the weight; greater is the velocity of fall. This statement is coherent with the really observed phenomena and, at present, is widespread among most part of the people living in the world. It is quite “natural” to believe that bodies cannot move without contact with a force (try to push a car with empty petrol tank!) and that heaviest bodies fall with the greatest velocity.
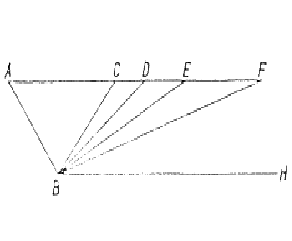
Aristotle’s approach seems indeed to work fine in many cases: if the difference between the density of the falling body and the density of the medium where it falls is small, the weight seems actually related to the velocity of downfall. (fig. 4) Aristotle’s theories lasted many centuries, even though they were modified during the Middle Ages. Here, we recall two interesting contributions: the “impetus” theory and the theorem of “average speed”. “Impetus” theory stated a body could move because of internal causes too: the “impetus”, stored inside the body, allows the body to move by itself, after the direct action of a force. The “average speed” theorem stated that the space covered by a body moving with uniform acceleration equals the space covered by a body moving with uniform velocity which is the average between the extreme velocities (at the beginning and at the end) of the first accelerated motion. At present, we consider this theorem an important result concerning any uniformly accelerated motion and, particularly, the fall of bodies: we relate it to the law of squared time in accelerated motions. Nevertheless, for philosophers and logicians living in the XIV° century, the theorem did not affect empirical phenomena, but only abstract quantities and qualities. 2) Galileo Let’s now skip centuries of history and let us give an account of Galileo’s model. First of all, let students face pendulum motion: it actually swings continuously but, after many oscillations, it does not reach the original height any more. Only an abstract pendulum could keep up the same height: this idealization is just Galileo’s pendulum. Following Galileo, a real pendulum is an ideal pendulum suffering disturbing effects: frictions, air resistance, Physical truth lies beyond bare phenomenology. This basic methodological and conceptual shift can be easily shown by means of a computer simulation which allows us to add or remove those disturbing effects. |
|||||
 |
 |
||||
| (Fig 5, 6: analogy between constrained pendulum motions and motions along inclined planes) | |||||
|
He made many experiments with great care, following two main hypotheses clashing against both common sense and Aristotelian physics: |
|||||
 |
 |
||||
Fig. 7Fig. 7 |
Fig. 8 |
||||
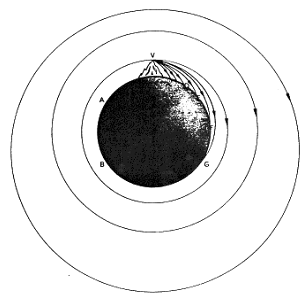
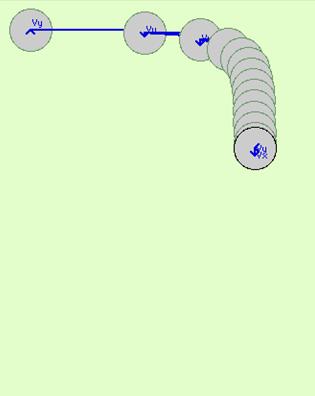
Other milestones of Aristotelian physics underwent Galileo’s criticism. Against Aristotle’s proportionality between force and velocity, Galileo stated a body can keep up its uniform motion in absence of whatever force. If the body stopped, this would be due to other forces which slow down the body. At present, we refer to this statement as to “Principle of Inertia”. Physics textbooks write: a body maintains its state of rest or rectilinear uniform motion until a force modifies this state. We should underline that we are not sure Galileo intended exactly “our“ Principle of Inertia when he spoke about motion in absence of forces. Scholars are in doubt: did Galileo refer just to our “rectilinear” uniform motion or to a more general “uniform” motion? We cannot discuss this subject here, but a short reading of Galileo’s original sources could be quite useful and interesting for students. At variance from ancient physics, in Galileo’s physics, motion, instead of rest, seems to be the main, “natural” character of the physics “story”. Together with the Principle of Inertia, in the Galileo’s last books, we find the so called “Principle of Relativity”. The content of this principle is: the laws of physics, as well as the results of experiments do not depend on the state of rectilinear uniform motion of the laboratory. Galileo suggested that we should make experiments under the deck of a ship: among them, he described some experiments about fall of bodies. Whether the ship is at rest in the harbor or it is traveling uniformly in the sea, objects fall along a vertical line. If we were not allowed to get a look outside the ship, how could we realize whether we are in motion or not? Of course, we should recall that the same doubts about “uniform” motion, affect Galileo’s Principle of Relativity as well as the Principle of Inertia. The last thing we would remind is the close relationship between Principle of Inertia and Principle of Relativity. This query, although out of the main subject of this paper, is quite important from the didactical point of view and would deserve our attention. |
|||||
|
Fig. 9 |
Fig. 10 |
||||
3) Newton
In 1642, when Galileo died, another great scientist, today as famous as Galileo, was born in Great Britain: I. Newton. He took important contributions to two different scientific traditions: the tradition of mathematical physics (mechanics, astronomy and hydrodynamics) and the tradition of experimental physics (optics, electricity, magnetism and thermo logy). In mechanics, he followed Galileo’s theories, but added a new perspective: the researches of the causes of motion. He defined these causes “forces”: they do modify the state of rest or rectilinear uniform motion (inertial motion) of bodies. All motions are the result of the action of two different kinds of force: the “vis insita” that tends to keep bodies at rest, or “inertial motion”, the “vis impressa” that tends to modify the state of motion. The Principle of Inertia became the first law of the three ones he established as foundation of mechanics. The second law states that force acting on a body makes it accelerate. For instance, the acceleration in the free fall requires a “fall” force, named “gravitational force”. The third law is the law of “action and reaction”. Although he accepted Galilean Principle of Relativity, he thought a coherent foundation of physics required the hypothesis of an “absolute space”, at absolute rest, existing in itself, neither connected to bodies nor to their motions. In his point of view, only an absolute space could save the truth of the Principle of Inertia. Beside usual space, belonging to our experience, and depending on the choice of the reference frame, the absolute space, unchangeable, endless and everlasting, only make us sure that the laws of physics are well established. |
|||||
Fig. 11 |
Fig. 12 |
||||
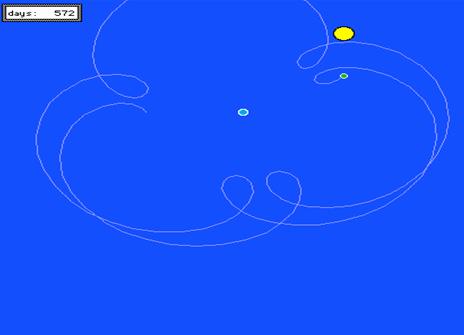
Newton’s theory of gravitation offered a wider frame to Galileo’s law of fall. Following Newton’s second law, the gravitational force experienced by a body equals the product between the body’s mass and its acceleration. On the other hand, the gravitational force depends on the mass too. In the case of gravitation, F = G0 m M / r2 and, in any case, F = m a (second law), where “m” is the mass of the body under consideration. We could say that more is the mass, more is the gravitational attraction; more is the mass, more is the inertial resistence to motion. Therefore, gravitational acceleration does not depend on the mass. In the neighborhood of the Earth’s surface, all bodies fall with the same acceleration. But, deepening the subject, we should say that the “mass” in the gravitational force is a “gravitational” mass, whilst the “mass” in the second law is an “inertial” mass. In the simple case of a single body nearby Earth’s surface, inertial mass equals gravitational mass but, in more complex systems, the part of the system corresponding to inertial mass might be different from the part corresponding to the gravitational mass, as Atwood’s machine shows. |
|||||
Fig. 13 |
Fig. 14 |
||||
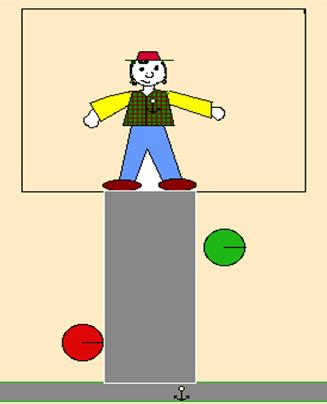
Facing a classroom, we should underline that Newton’s theory of “fall” is quite sophisticated and rich in hypotheses. This fact should be compared with the famous Newton’s statement: “Hypotheses non fingo” (I do not make hypotheses). 4) Einstein Mach criticism had a deep influence on the young Einstein. Once again, in the same year - 1879 - when one of the greatest physicists (J.C. Maxwell) of XIX° century died, A. Einstein was born. In 1905, he wrote three fundamental papers on the most difficult queries of contemporary physics: since then, those papers have been considered milestones in the history of physics. One of them concerned the relationship between mechanics and electromagnetism. Einstein’s theory, today known as Theory of Special Relativity, accepted Maxwell’s electromagnetic theory and modified Newton’s mechanics. It is a quite sophisticated theory, which clashes against common sense and emphasizes some amazing symmetries: between space and time and between electricity and magnetism. Many important predictions follow; among them, we remind the equivalence between mass and energy, a relationship widely known and published. This equivalence raises a question: if the kinetic energy of a body affects its inertial mass, then its inertial mass might be different from its gravitational mass. We should accept that bodies with different velocities fall with different accelerations. This contradicts both Galileo’s and Newton’s laws of fall. Coherently with the results of some experiments (Eötvos), Einstein decided to define as “principle” the hypothesis of the identity between inertial mass and gravitational mass. In 1907, he suggested a conceptual experiment which led him to state the Equivalence Principle: a gravitational field is locally equivalent to acceleration. The fact is that experiments performed inside a box do not allow us to state whether we are inside an inertial reference frame placed in a gravitational field or we are in a non-inertial reference frame. We suggest to the students two different situations, described below. |
|||||
Fig. 15 |
Fig. 16 |
||||
In the laboratory (the box), bodies do not weight. It is the effect of a free fall in a gravitational field OR the effect of an inertial motion in empty space? Now, bodies are “heavy”: they fall. Is it the gravitational effect of a cosmic body close to the laboratory OR the effect of an “upward” acceleration in empty space? In 1916, Einstein brought out his theory of gravitation, from then named General Theory of Relativity. In this theory, space and time depend on the arrangement of masses and the “fall” of bodies acquires a new meaning. The effect of the masses is usually explained in terms of “forces” bending the inertial motion of bodies. Einstein suggested masses could modify the geometry of space-time: instead of forces acting in a “flat” quasi-Euclidean space-time, he assumed simply a curved space-time. The bending of space-time is just due to masses. Because of its formal beauty, Einstein’s theory of gravitation had immediately a great success, even though corroborated by only few experiments: among there, we would like to remind the “fall” of light, namely the bending of light rays traveling close to sun.
Fig. 17 |
|||||
Which end for the story?
We have no end for our story: probably, in the future, other characters will join Aristotle, Galileo, Newton and Einstein. There is neither final happy end nor ultimate truth. History of physics offers us a stage where alternative interpretations lead us to better understand the world. Learning these alternative interpretations is the only way to learn physics in a non-trivial way. Even though these different interpretations are not equivalent in a strict sense, we might say that, inside their own range, they are “good” explanations. Now, we have, in front of us, four different points of view from which consider the motion of arrows, projectiles and satellites. |
|||||
Aristotle |
Galileo |
Newton |
Einstein |
||
“relational” space geocentric system forces acting by contact
velocity prop. to weight |
mathematics & experim.
heliocentric system compound motions Principle of Inertia and law of acceler. motion |
“ absolute” space
“vis insita” & “vis impr.”
law of universal gravit. fall of bodies = satellites |
“ relational” space geometriz. of physics mass is energy
Equivalence Principle “bending” of light rays |
||
Of course, many queries quoted in this paper would deserve more attention than that required from a didactical “story”. We have not enough space on this paper. We have not enough space to talk about ethic and aesthetic values of scientific theories too. We would only like to point out how useful are, in our approach, multimedial and hypermedial tools. |
|||||


 7
7